我们已经在 4.1节中描述了多层感知机（MLP）， 现在让我们尝试自己实现一个多层感知机。 为了与之前softmax回归（ 3.6节 ） 获得的结果进行比较， 我们将继续使用Fashion-MNIST图像分类数据集 （ 3.5节）。

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化模型参数

回想一下，Fashion-MNIST中的每个图像由 28×28=784个灰度像素值组成。 所有图像共分为10个类别。 忽略像素之间的空间结构， 我们可以将每个图像视为具有784个输入特征 和10个类的简单分类数据集。 首先，我们将实现一个具有单隐藏层的多层感知机， 它包含256个隐藏单元。 注意，我们可以将这两个变量都视为超参数。 通常，我们选择2的若干次幂作为层的宽度。 因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。

我们用几个张量来表示我们的参数。 注意，对于每一层我们都要记录一个权重矩阵和一个偏置向量。 跟以前一样，我们要为损失关于这些参数的梯度分配内存。

num_inputs, num_outputs, num_hiddens = 784, 10, 256

W1 = nn.Parameter(torch.randn(
    num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(
    num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

激活函数

为了确保我们对模型的细节了如指掌， 我们将实现ReLU激活函数， 而不是直接调用内置的relu函数。

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

模型

因为我们忽略了空间结构， 所以我们使用reshape将每个二维图像转换为一个长度为num_inputs的向量。 只需几行代码就可以实现我们的模型。

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

损失函数

由于我们已经从零实现过softmax函数（ 3.6节）， 因此在这里我们直接使用高级API中的内置函数来计算softmax和交叉熵损失。 回想一下我们之前在 3.7.2节中 对这些复杂问题的讨论。 我们鼓励感兴趣的读者查看损失函数的源代码，以加深对实现细节的了解

loss = nn.CrossEntropyLoss(reduction='none')

训练

optimizer = torch.optim.SGD(params, lr=0.001)
for epoch in range(30):  # 100个epoch作为示例
    running_loss = 0.0
    for i, data in enumerate(tqdm(train_iter, 0)):
        inputs, labels = data
        # print(inputs.shape)
        # print(labels.shape)
        optimizer.zero_grad()
        outputs = net(inputs)
        loss = criterion(outputs,labels).sum()
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if i % 200 == 199:    # 每200个小批量打印一次
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 200))
            running_loss = 0.0

print('Finished Training')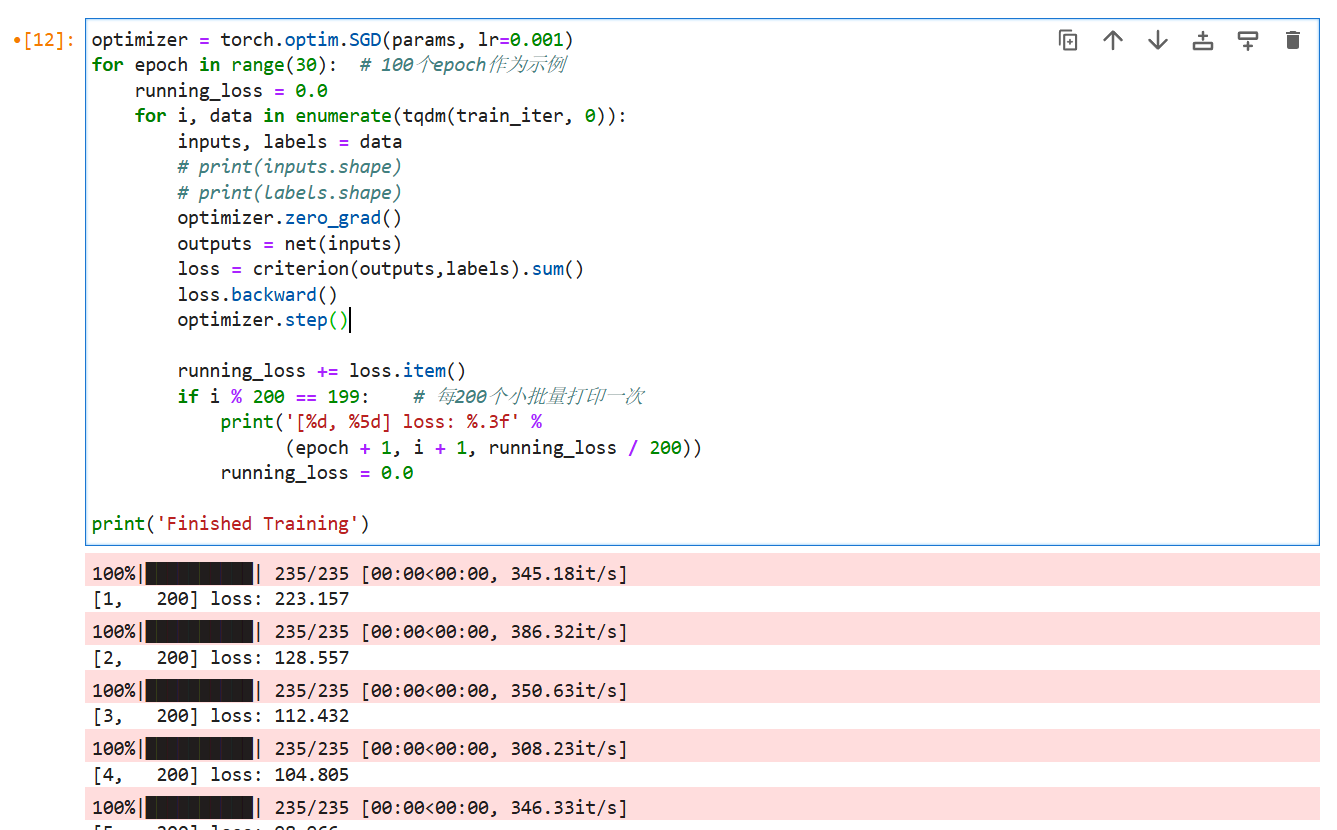

为了对学习到的模型进行评估，我们将在一些测试数据上应用这个模型。

# 测试网络
correct = 0
total = 0
with torch.no_grad():
    for data in test_iter:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))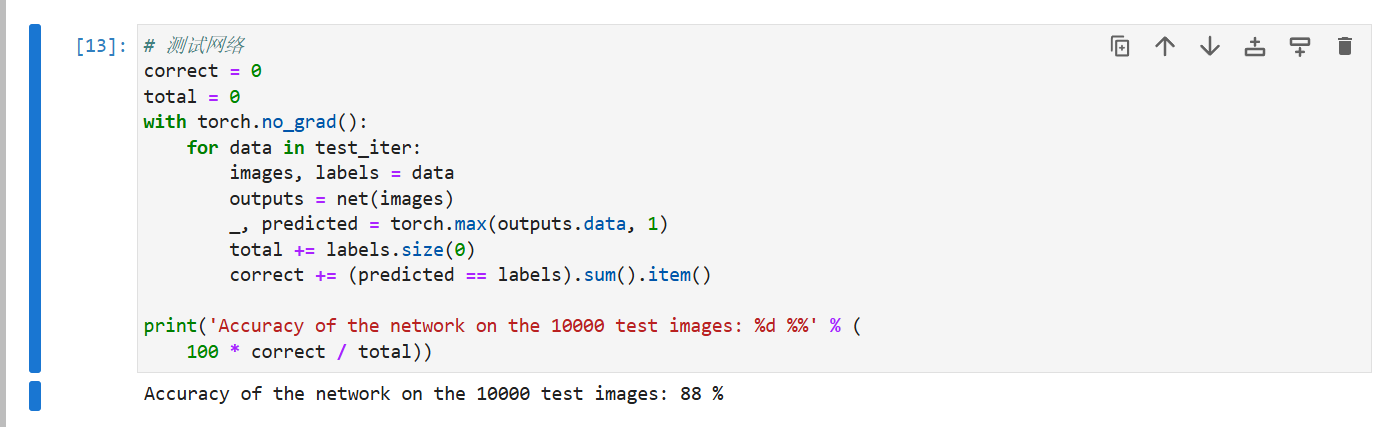

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

小结

• 手动实现一个简单的多层感知机是很容易的。然而如果有大量的层，从零开始实现多层感知机会变得很麻烦（例如，要命名和记录模型的参数）。

练习

1.在所有其他参数保持不变的情况下，更改超参数num_hiddens的值，并查看此超参数的变化对结果有何影响。确定此超参数的最佳值。

2.尝试添加更多的隐藏层，并查看它对结果有何影响。

3.改变学习速率会如何影响结果？保持模型架构和其他超参数（包括轮数）不变，学习率设置为多少会带来最好的结果？

4.通过对所有超参数（学习率、轮数、隐藏层数、每层的隐藏单元数）进行联合优化，可以得到的最佳结果是什么？

5.描述为什么涉及多个超参数更具挑战性。

6.如果想要构建多个超参数的搜索方法，请想出一个聪明的策略。