在 3.3节中， 我们发现通过深度学习框架的高级API能够使实现

线性回归变得更加容易。 同样，通过深度学习框架的高级API也能更方便地实现softmax回归模型。 本节如在 3.6节中一样， 继续使用Fashion-MNIST数据集，并保持批量大小为256。

import torch
from torch import nn
from d2l import torch as d2l
from tqdm import tqdm

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化模型参数

如我们在 3.4节所述， softmax回归的输出层是一个全连接层。 因此，为了实现我们的模型， 我们只需在Sequential中添加一个带有10个输出的全连接层。 同样，在这里Sequential并不是必要的， 但它是实现深度模型的基础。 我们仍然以均值0和标准差0.01随机初始化权重。

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

1. def init_weights(m): 定义了一个名为 init_weights 的函数，这个函数接受一个参数 m，它代表模型中的一个模块（例如层或子层）。

2. if type(m) == nn.Linear: 这行代码检查传入的模块 m 是否是 nn.Linear 类型的实例。nn.Linear 是 PyTorch 中用于实现全连接层（即线性层）的类。

3. nn.init.normal_(m.weight, std=0.01) 如果模块 m 是线性层，这行代码将使用正态分布初始化该层的权重。nn.init.normal_ 是 PyTorch 提供的一个函数，用于将张量用正态分布的值进行初始化。这里的 std=0.01 表示正态分布的标准差为0.01，权重值将从均值为0的正态分布中随机采样。

4. net.apply(init_weights) 这行代码将 init_weights 函数应用到模型 net 的所有模块上。apply 是 PyTorch 中 nn.Module 类的一个方法，它递归地遍历模型的所有子模块，并将传入的函数应用于每个子模块。在这个例子中，init_weights 函数将被应用于 net 模型中的每个子模块，如果子模块是线性层，就会对其进行权重初始化。

重新审视softmax的实现

在前面 3.6节的例子中， 我们计算了模型的输出，然后将此输出送入交叉熵损失。 从数学上讲，这是一件完全合理的事情。 然而，从计算角度来看，指数可能会造成数值稳定性问题。

我们也希望保留传统的softmax函数，以备我们需要评估通过模型输出的概率。 但是，我们没有将softmax概率传递到损失函数中， 而是在交叉熵损失函数中传递未规范化的预测，并同时计算softmax及其对数， 这是一种类似“LogSumExp技巧”的聪明方式。

loss = nn.CrossEntropyLoss(reduction='none')

在 PyTorch 中，reduction 参数有以下几种选项：

1. 'none'：不进行任何缩减，返回每个样本的损失。

2. 'mean'：将所有样本的损失求平均值。

3. 'sum'：将所有样本的损失求和。

当设置为 'none' 时，nn.CrossEntropyLoss 将返回一个与输入样本数量相同长度的张量，其中每个元素代表对应样本的损失值。这样，你可以对每个样本的损失进行单独处理，例如在某些情况下可能需要对不同样本的损失进行加权。

举个例子，假设你有一个包含3个样本的批次，每个样本有5个类别的预测概率，真实标签为类别索引。使用 nn.CrossEntropyLoss(reduction='none') 时，你将得到一个长度为3的张量，其中每个元素是对应样本的损失值。这样，你可以进一步对这些损失值进行操作，比如计算加权平均或进行其他形式的缩减。

优化算法

在这里，我们使用学习率为0.1的小批量随机梯度下降作为优化算法。 这与我们在线性回归例子中的相同，这说明了优化器的普适性。

trainer = torch.optim.SGD(net.parameters(), lr=0.01)

训练

for epoch in range(30):  # 100个epoch作为示例
    running_loss = 0.0
    for i, data in enumerate(tqdm(train_iter, 0)):
        inputs, labels = data
        # print(inputs.shape)
        # print(labels.shape)
        optimizer.zero_grad()
        outputs = net(inputs)
        loss = criterion(outputs,labels).sum()
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if i % 200 == 199:    # 每200个小批量打印一次
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 200))
            running_loss = 0.0

print('Finished Training')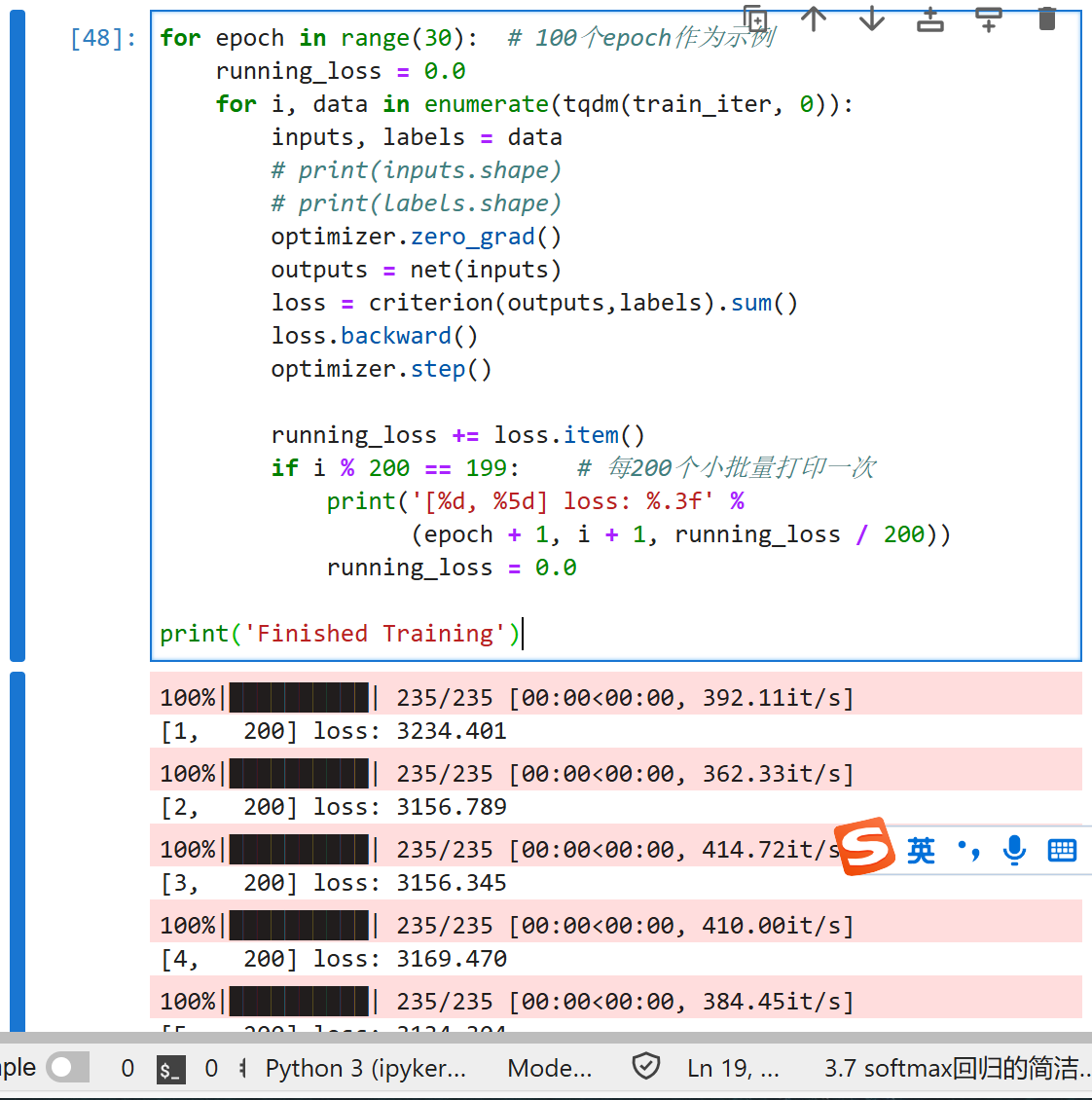

和以前一样，这个算法使结果收敛到一个相当高的精度，而且这次的代码比之前更精简了。

精度

# 测试网络
correct = 0
total = 0
with torch.no_grad():
    for data in test_iter:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))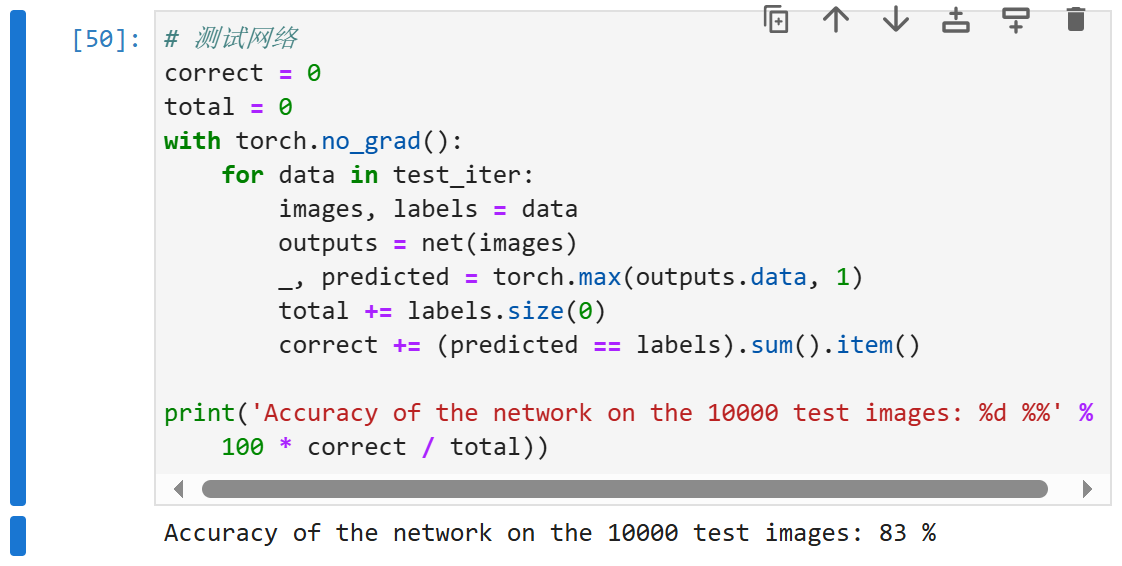

小结

• 使用深度学习框架的高级API，我们可以更简洁地实现softmax回归。

• 从计算的角度来看，实现softmax回归比较复杂。在许多情况下，深度学习框架在这些著名的技巧之外采取了额外的预防措施，来确保数值的稳定性。这使我们避免了在实践中从零开始编写模型时可能遇到的陷阱。

练习

1.尝试调整超参数，例如批量大小、迭代周期数和学习率，并查看结果。

2.增加迭代周期的数量。为什么测试精度会在一段时间后降低？我们怎么解决这个问题？

QA