在 3.1节中我们介绍了线性回归。 随后，在 3.2节中我们从头实现线性回归。 然后，在 3.3节中我们使用深度学习框架的高级API简洁实现线性回归。

回归可以用于预测多少的问题。 比如预测房屋被售出价格，或者棒球队可能获得的胜场数，又或者患者住院的天数。

事实上，我们也对分类问题感兴趣：不是问“多少”，而是问“哪一个”：

• 某个电子邮件是否属于垃圾邮件文件夹？

• 某个用户可能注册或不注册订阅服务？

• 某个图像描绘的是驴、狗、猫、还是鸡？

• 某人接下来最有可能看哪部电影？

通常，机器学习实践者用分类这个词来描述两个有微妙差别的问题： 1. 我们只对样本的“硬性”类别感兴趣，即属于哪个类别； 2. 我们希望得到“软性”类别，即得到属于每个类别的概率。 这两者的界限往往很模糊。其中的一个原因是：即使我们只关心硬类别，我们仍然使用软类别的模型。

分类问题

网络架构

为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。 为了解决线性模型的分类问题，我们需要和输出一样多的仿射函数（affine function）。 每个输出对应于它自己的仿射函数。 在我们的例子中，由于我们有4个特征和3个可能的输出类别， 我们将需要12个标量来表示权重（带下标的w）， 3个标量来表示偏置（带下标的b）。 下面我们为每个输入计算三个未规范化的预测（logit）：o_1、o_2和o_3

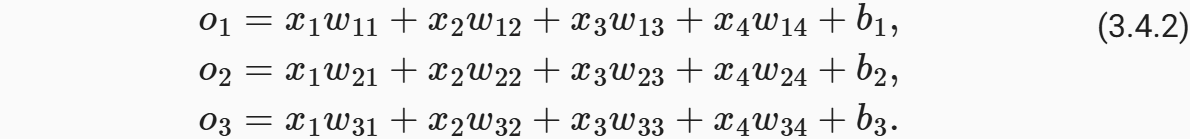
我们可以用神经网络图 图3.4.1来描述这个计算过程。 与线性回归一样，softmax回归也是一个单层神经网络。 由于计算每个输出o_1、o_2和o_3取决于 所有输入x_1、x_2、x_3和x_4， 所以softmax回归的输出层也是全连接层。

为了更简洁地表达模型，我们仍然使用线性代数符号。 通过向量形式表达为o=Wx+b， 这是一种更适合数学和编写代码的形式。 由此，我们已经将所有权重放到一个3×4矩阵中。 对于给定数据样本的特征x， 我们的输出是由权重与输入特征进行矩阵-向量乘法再加上偏置b得到的。

全连接层的参数开销

正如我们将在后续章节中看到的，在深度学习中，全连接层无处不在。 然而，顾名思义，全连接层是“完全”连接的，可能有很多可学习的参数。 具体来说，对于任何具有d个输入和q个输出的全连接层， 参数开销为O(dq)，这个数字在实践中可能高得令人望而却步。 幸运的是，将d个输入转换为q个输出的成本可以减少到O(\frac{dq}{n})， 其中超参数n可以由我们灵活指定，以在实际应用中平衡参数节约和模型有效性 (Zhang et al., 2021)。

softmax运算

现在我们将优化参数以最大化观测数据的概率。 为了得到预测结果，我们将设置一个阈值，如选择具有最大概率的标签。

我们希望模型的输出为\hat y_j可以视为属于类为j的概率， 然后选择具有最大输出值的类别为argmax_jy_j作为我们的预测。 例如，如果\hat y_1、\hat y_2和\hat y_3分别为0.1、0.8和0.1， 那么我们预测的类别是2，在我们的例子中代表“鸡”。

然而我们能否将未规范化的预测o直接视作我们感兴趣的输出呢？ 答案是否定的。 因为将线性层的输出直接视为概率时存在一些问题： 一方面，我们没有限制这些输出数字的总和为1。 另一方面，根据输入的不同，它们可以为负值。 这些违反了 2.6节中所说的概率基本公理。

要将输出视为概率，我们必须保证在任何数据上的输出都是非负的且总和为1。 此外，我们需要一个训练的目标函数，来激励模型精准地估计概率。 例如， 在分类器输出0.5的所有样本中，我们希望这些样本是刚好有一半实际上属于预测的类别。 这个属性叫做校准（calibration）。

小批量样本的矢量化

损失函数

接下来，我们需要一个损失函数来度量预测的效果。 我们将使用最大似然估计，这与在线性回归 （ 3.1.3节） 中的方法相同。

L2 Loss

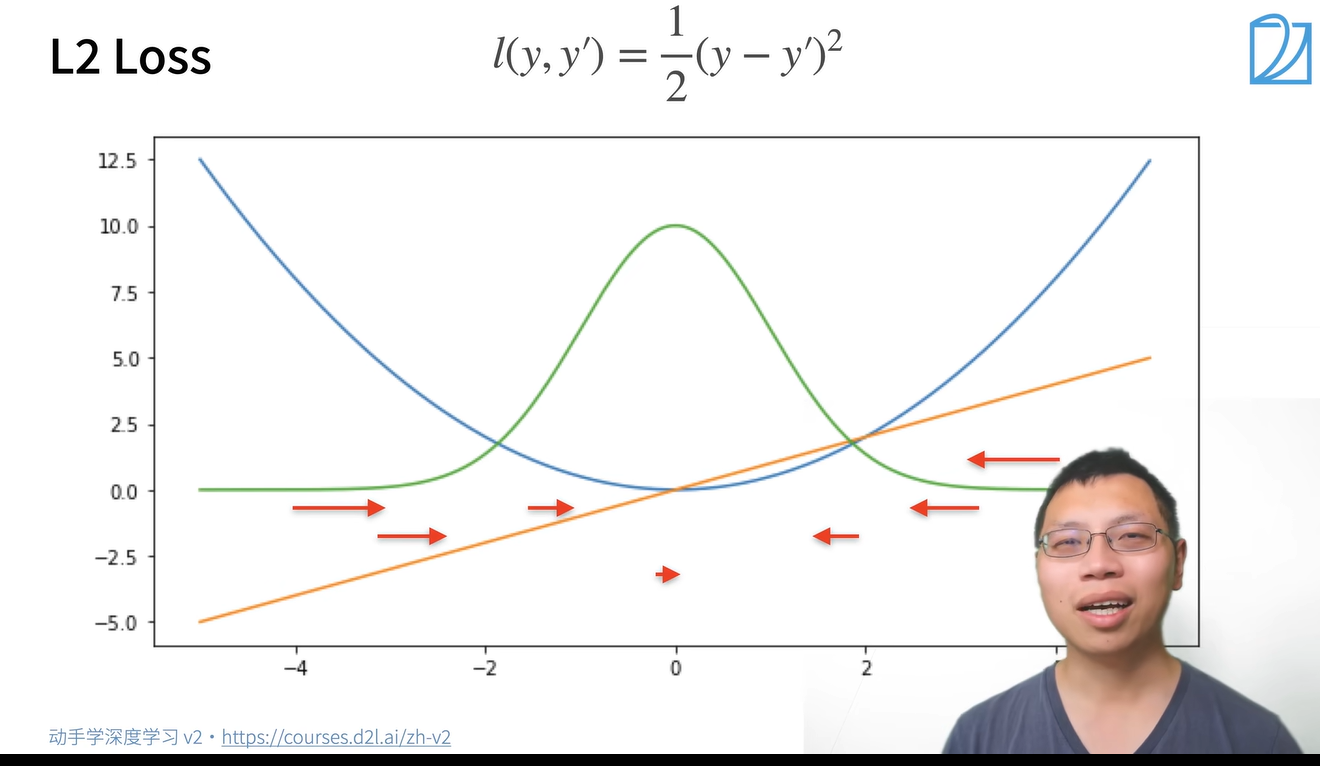
注：绿色的线是似然函数

• 对异常值非常敏感，因为异常值的影响是平方的，这可能导致模型对异常值的过度拟合。

• 倾向于产生平滑解，所有系数通常都不会为零，这可能导致过拟合。

• 优化时可能需要更复杂的算法，如梯度下降。

L1 Loss

• 特点：

  • 对异常值不敏感，因为异常值的影响是线性的。

  • 倾向于产生稀疏解，即在特征选择中，很多系数可能为零，这有助于特征选择。

  • 计算简单，易于优化。

Huber's Robust Loss

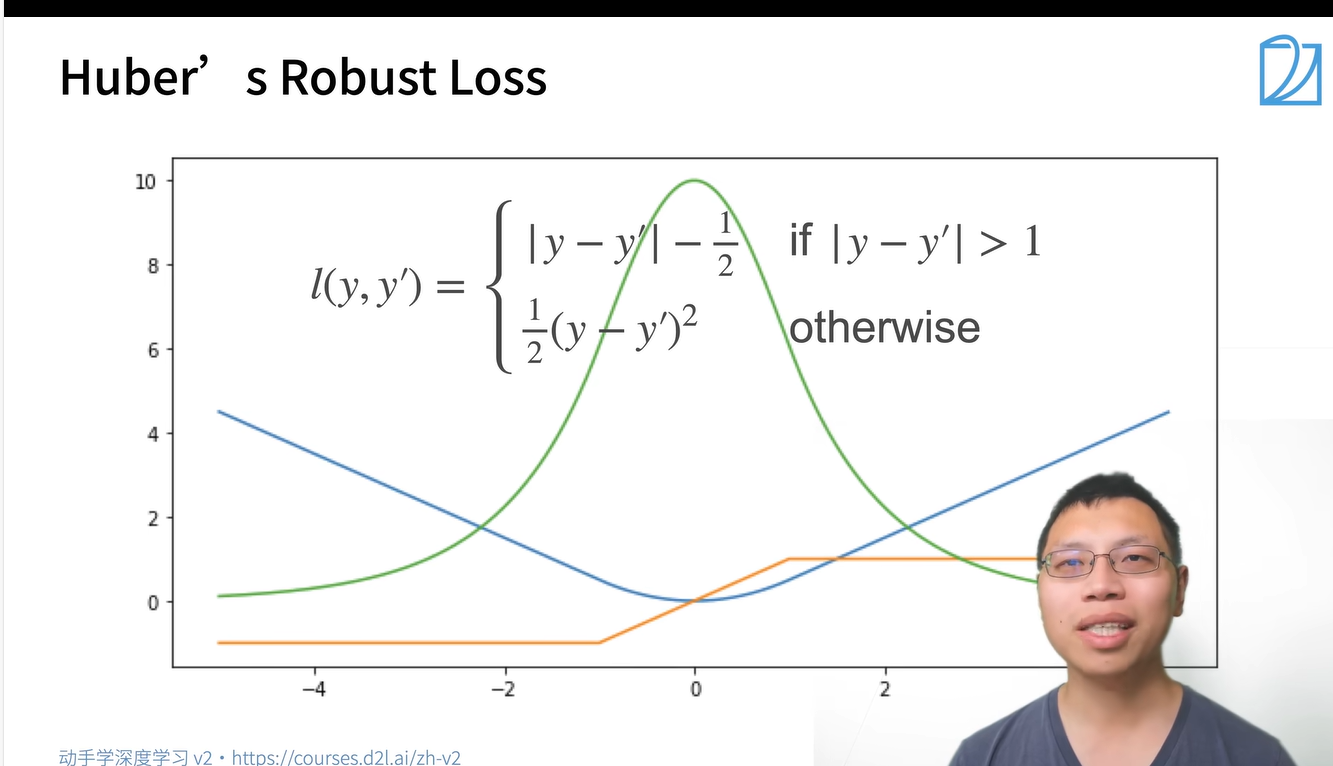
对数似然

在本节稍后的内容会讲到， (3.4.8)中的损失函数 通常被称为交叉熵损失（cross-entropy loss）。 由于y是一个长度为q的独热编码向量， 所以除了一个项以外的所有项j都消失了。 由于所有\hat y_j都是预测的概率，所以它们的对数永远不会大于0。 因此，如果正确地预测实际标签，即如果实际标签P(y|x)=1， 则损失函数不能进一步最小化。 注意，这往往是不可能的。 例如，数据集中可能存在标签噪声（比如某些样本可能被误标）， 或输入特征没有足够的信息来完美地对每一个样本分类。

softmax及其导数

由于softmax和相关的损失函数很常见， 因此我们需要更好地理解它的计算方式。 将 (3.4.3)代入损失 (3.4.8)中。 利用softmax的定义，我们得到：

换句话说，导数是我们softmax模型分配的概率与实际发生的情况（由独热标签向量表示）之间的差异。 从这个意义上讲，这与我们在回归中看到的非常相似， 其中梯度是观测值y和估计值y^之间的差异。 这不是巧合，在任何指数族分布模型中 （参见本书附录中关于数学分布的一节）， 对数似然的梯度正是由此得出的。 这使梯度计算在实践中变得容易很多。

交叉熵损失

现在让我们考虑整个结果分布的情况，即观察到的不仅仅是一个结果。 对于标签y，我们可以使用与以前相同的表示形式。 唯一的区别是，我们现在用一个概率向量表示，如(0.1,0.2,0.7)， 而不是仅包含二元项的向量(0,0,1)。 我们使用 (3.4.8)来定义损失l， 它是所有标签分布的预期损失值。 此损失称为交叉熵损失（cross-entropy loss），它是分类问题最常用的损失之一。 本节我们将通过介绍信息论基础来理解交叉熵损失。 如果想了解更多信息论的细节，请进一步参考 本书附录中关于信息论的一节。

信息论基础

信息论（information theory）涉及编码、解码、发送以及尽可能简洁地处理信息或数据。

熵

信息量

压缩与预测有什么关系呢？ 想象一下，我们有一个要压缩的数据流。 如果我们很容易预测下一个数据，那么这个数据就很容易压缩。 为什么呢？ 举一个极端的例子，假如数据流中的每个数据完全相同，这会是一个非常无聊的数据流。 由于它们总是相同的，我们总是知道下一个数据是什么。 所以，为了传递数据流的内容，我们不必传输任何信息。也就是说，“下一个数据是xx”这个事件毫无信息量。

重新审视交叉熵

模型预测和评估

在训练softmax回归模型后，给出任何样本特征，我们可以预测每个输出类别的概率。 通常我们使用预测概率最高的类别作为输出类别。 如果预测与实际类别（标签）一致，则预测是正确的。 在接下来的实验中，我们将使用精度（accuracy）来评估模型的性能。 精度等于正确预测数与预测总数之间的比率。

小结

• softmax运算获取一个向量并将其映射为概率。

• softmax回归适用于分类问题，它使用了softmax运算中输出类别的概率分布。

• 交叉熵是一个衡量两个概率分布之间差异的很好的度量，它测量给定模型编码数据所需的比特数。

练习