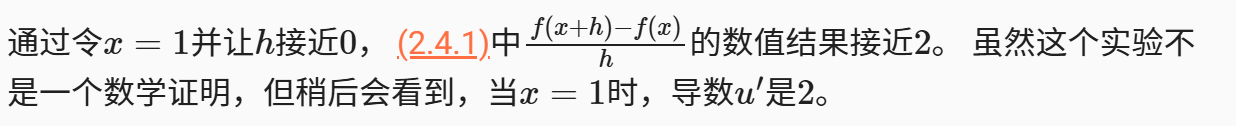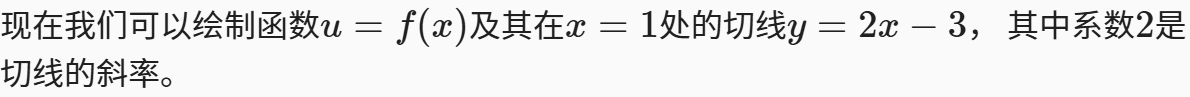本文最后更新于 2024-11-14，文章内容可能已经过时。

在2500年前，古希腊人把一个多边形分成三角形，并把它们的面积相加，才找到计算多边形面积的方法。 为了求出曲线形状（比如圆）的面积，古希腊人在这样的形状上刻内接多边形。 如 图2.4.1所示，内接多边形的等长边越多，就越接近圆。 这个过程也被称为逼近法（method of exhaustion）。


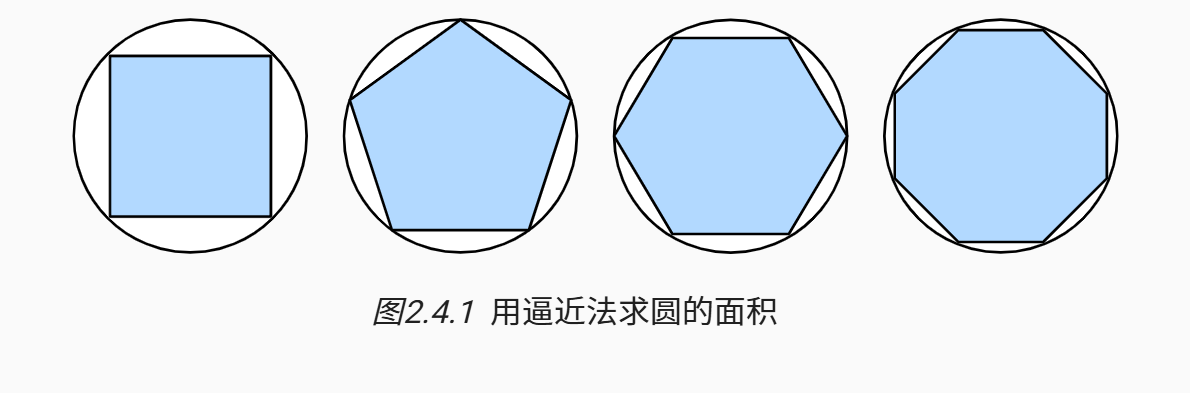
事实上，逼近法就是积分（integral calculus）的起源。 2000多年后，微积分的另一支，微分（differential calculus）被发明出来。 在微分学最重要的应用是优化问题，即考虑如何把事情做到最好。 正如在 2.3.10.1节中讨论的那样， 这种问题在深度学习中是无处不在的。

在深度学习中，我们“训练”模型，不断更新它们，使它们在看到越来越多的数据时变得越来越好。 通常情况下，变得更好意味着最小化一个损失函数（loss function）， 即一个衡量“模型有多糟糕”这个问题的分数。 最终，我们真正关心的是生成一个模型，它能够在从未见过的数据上表现良好。 但“训练”模型只能将模型与我们实际能看到的数据相拟合。 因此，我们可以将拟合模型的任务分解为两个关键问题：

  • 优化（optimization）：用模型拟合观测数据的过程；

  • 泛化（generalization）：数学原理和实践者的智慧，能够指导我们生成出有效性超出用于训练的数据集本身的模型。

为了帮助读者在后面的章节中更好地理解优化问题和方法， 本节提供了一个非常简短的入门教程，帮助读者快速掌握深度学习中常用的微分知识。

导数和微分

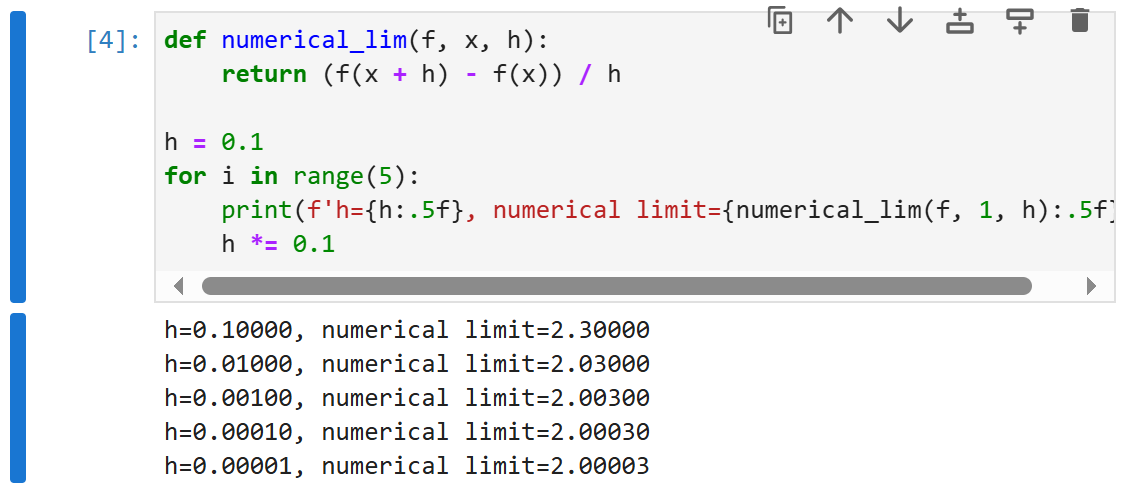
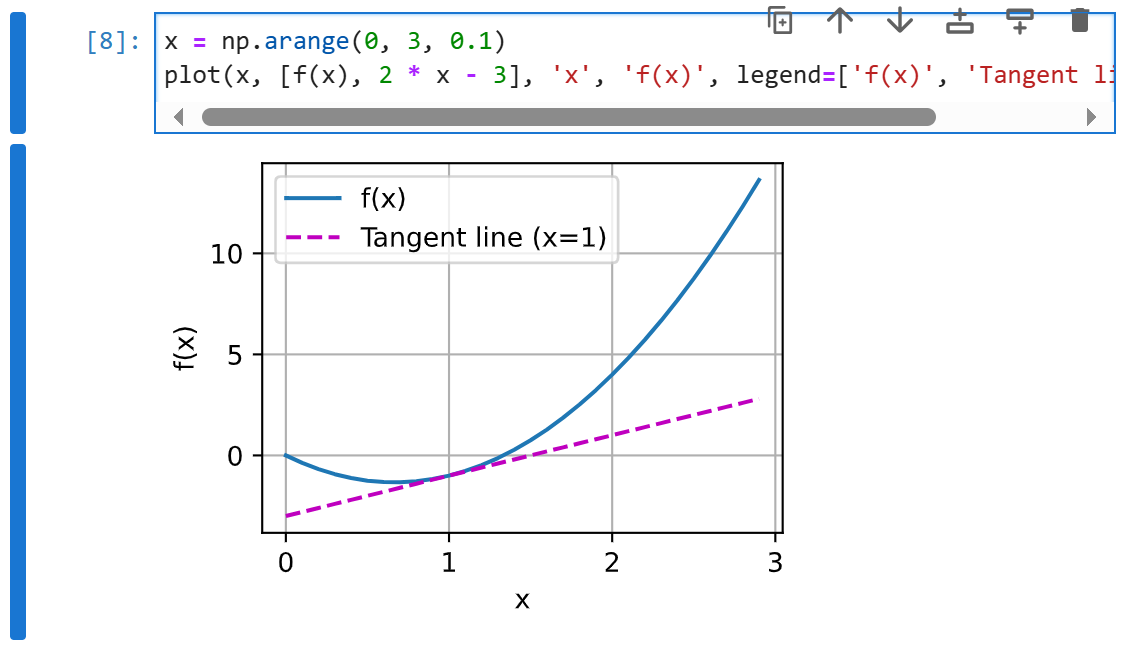
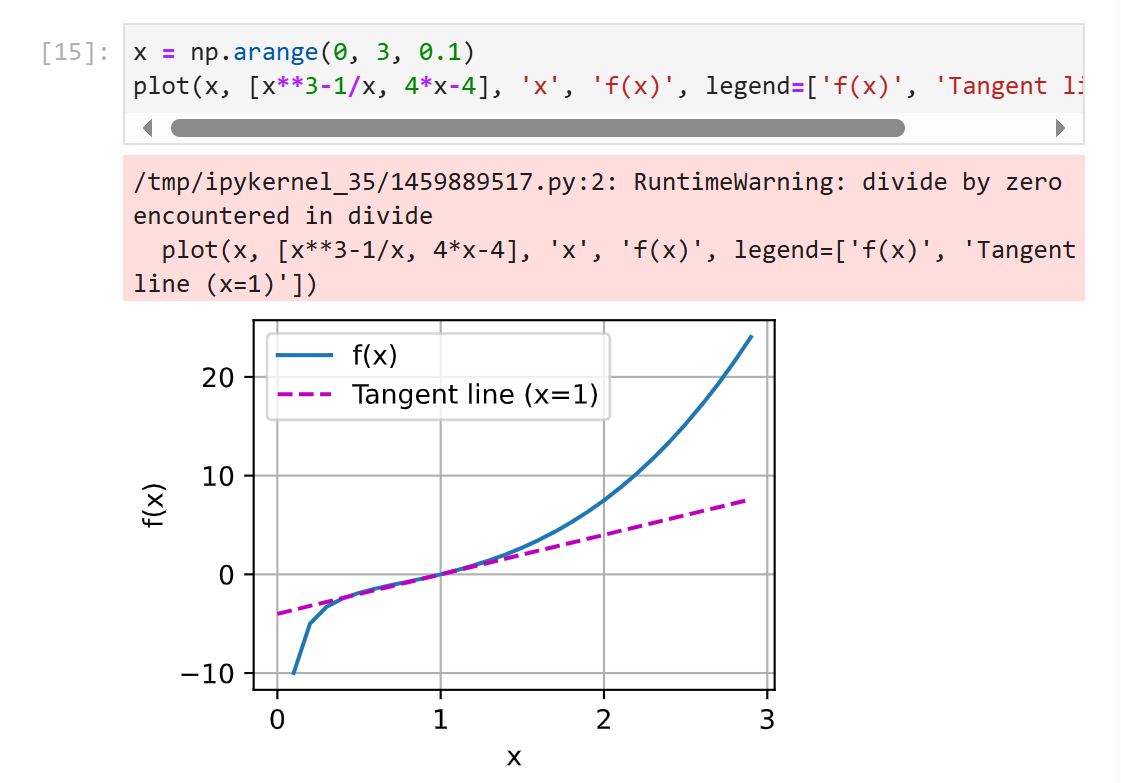
我们首先讨论导数的计算，这是几乎所有深度学习优化算法的关键步骤。 在深度学习中，我们通常选择对于模型参数可微的损失函数。 简而言之，对于每个参数， 如果我们把这个参数增加或减少一个无穷小的量，可以知道损失会以多快的速度增加或减少，

%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l


def f(x):
    return 3 * x ** 2 - 4 * x
Python

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

h = 0.1
for i in range(5):
    print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
    h *= 0.1
Python

为了对导数的这种解释进行可视化，我们将使用matplotlib， 这是一个Python中流行的绘图库。 要配置matplotlib生成图形的属性，我们需要定义几个函数。 在下面，use_svg_display函数指定matplotlib软件包输出svg图表以获得更清晰的图像。

注意，注释#@save是一个特殊的标记，会将对应的函数、类或语句保存在d2l包中。 因此，以后无须重新定义就可以直接调用它们（例如，d2l.use_svg_display()）。

def use_svg_display():  #@save
    """使用svg格式在Jupyter中显示绘图"""
    backend_inline.set_matplotlib_formats('svg')
Python

我们定义set_figsize函数来设置图表大小。 注意，这里可以直接使用d2l.plt，因为导入语句 from matplotlib import pyplot as plt已标记为保存到d2l包中。

def set_figsize(figsize=(3.5, 2.5)):  #@save
    """设置matplotlib的图表大小"""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize
Python

下面的set_axes函数用于设置由matplotlib生成图表的轴的属性。

#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """设置matplotlib的轴"""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()
Python

通过这三个用于图形配置的函数，定义一个plot函数来简洁地绘制多条曲线， 因为我们需要在整个书中可视化许多曲线。

#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """绘制数据点"""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # 如果X有一个轴，输出True
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
Python

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
Python

偏导数

到目前为止，我们只讨论了仅含一个变量的函数的微分。 在深度学习中，函数通常依赖于许多变量。 因此，我们需要将微分的思想推广到多元函数（multivariate function）上。

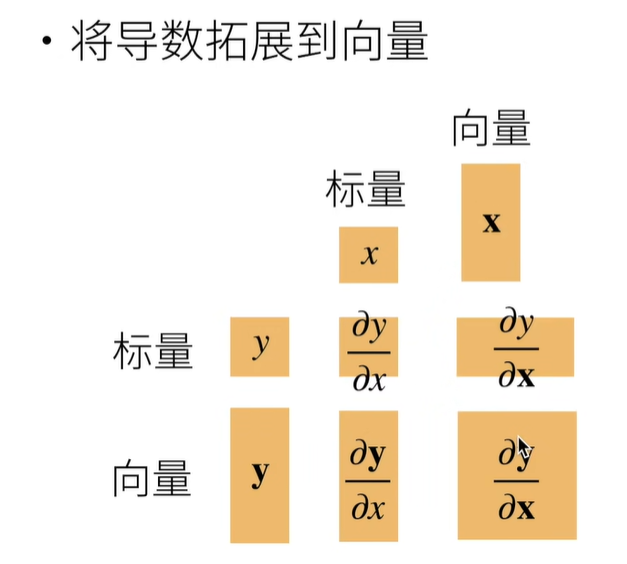
梯度

分子布局：

链式法则

然而，上面方法可能很难找到梯度。 这是因为在深度学习中，多元函数通常是复合（composite）的， 所以难以应用上述任何规则来微分这些函数。 幸运的是，链式法则可以被用来微分复合函数。

小结

  • 微分和积分是微积分的两个分支，前者可以应用于深度学习中的优化问题。

  • 导数可以被解释为函数相对于其变量的瞬时变化率，它也是函数曲线的切线的斜率。

  • 梯度是一个向量，其分量是多变量函数相对于其所有变量的偏导数。

  • 链式法则可以用来微分复合函数。

练习

1.

x = np.arange(0, 3, 0.1)
plot(x, [x**3-1/x, 4*x-4], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
Python

2.

[6x1,5ex2]\left[6x_{1}, 5e^{x^{2}}\right]

3.

4.

∂u∂a=∂u∂x∂x∂a+∂u∂y∂y∂a+∂u∂z∂z∂a\frac{\partial u}{\partial a}=\frac{\partial u}{\partial x}\frac{\partial x}{\partial a}+\frac{\partial u}{\partial y}\frac{\partial y}{\partial a}+\frac{\partial u}{\partial z}\frac{\partial z}{\partial a}